Fair Outsourcing Polynomial Computation Based on the Blockchain
Abstract
Due to the big data blowout from the Internet of Things and the rapid development of cloud computing, outsourcing computation has received considerable attention in recent years. Particularly, many outsourcing computation schemes have been proposed to dedicate the outsourcing polynomial computation due to its use in numerous fields, such as data analysis and machine learning. However, none of those schemes are practical enough, as they either require some time-consuming cryptographic operations to achieve fairness between the user and the worker, or cannot allow the user to outsource arbitrary polynomial to the worker, or need two non-collusive workers. To tackle these challenges, in this paper, we propose a new outsourcing polynomial computation scheme by employing a variant of Horner’s method and the blockchain technology. Specifically, the former makes the computational cost on the worker side as low as possible, and the latter guarantees the fairness between the user and the worker if the result from the worker can be publicly verified. To achieve the public verifiability property, we apply the sampling technique, which is effective in our proposal according to a game-theoretic analysis. Furthermore, we also implement a prototype of our proposal and run it on an Ethereum test net. The extensive experimental results demonstrate that our proposal is efficient in terms of computational cost.
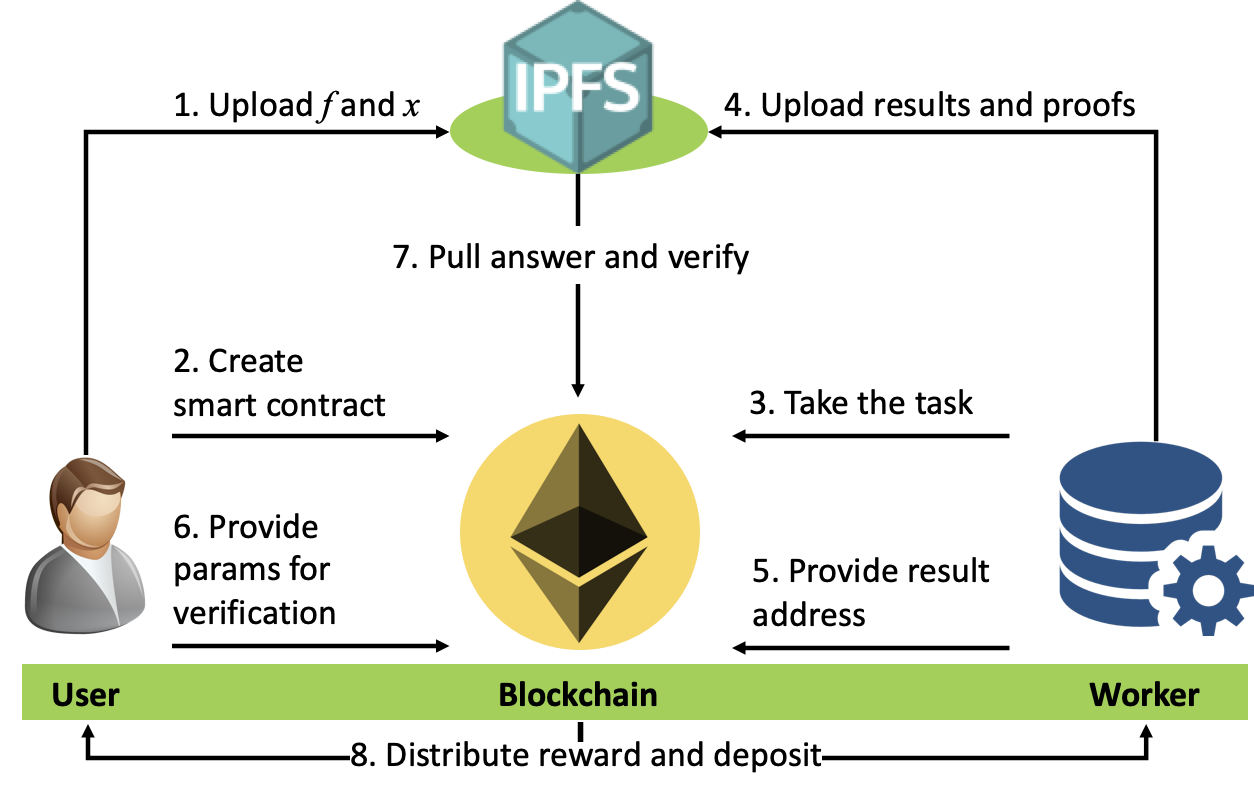
System Model and Design Goals
Design Goals
- Design a fair outsourcing polynomial computation scheme.
- The proposed scheme should be efficient.
- The proposed scheme should support arbitrary polynomials.
- The proposed scheme should support reusability.
When $f(x) = \sum_{i = 0}^n a_i x^i$ Is a Univariate Polynomial
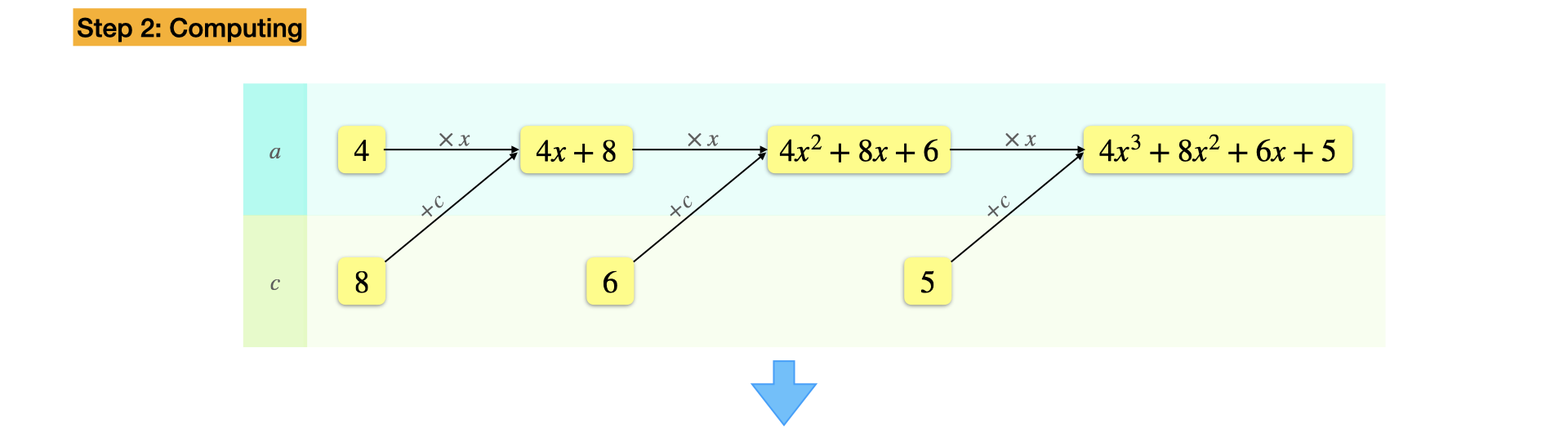
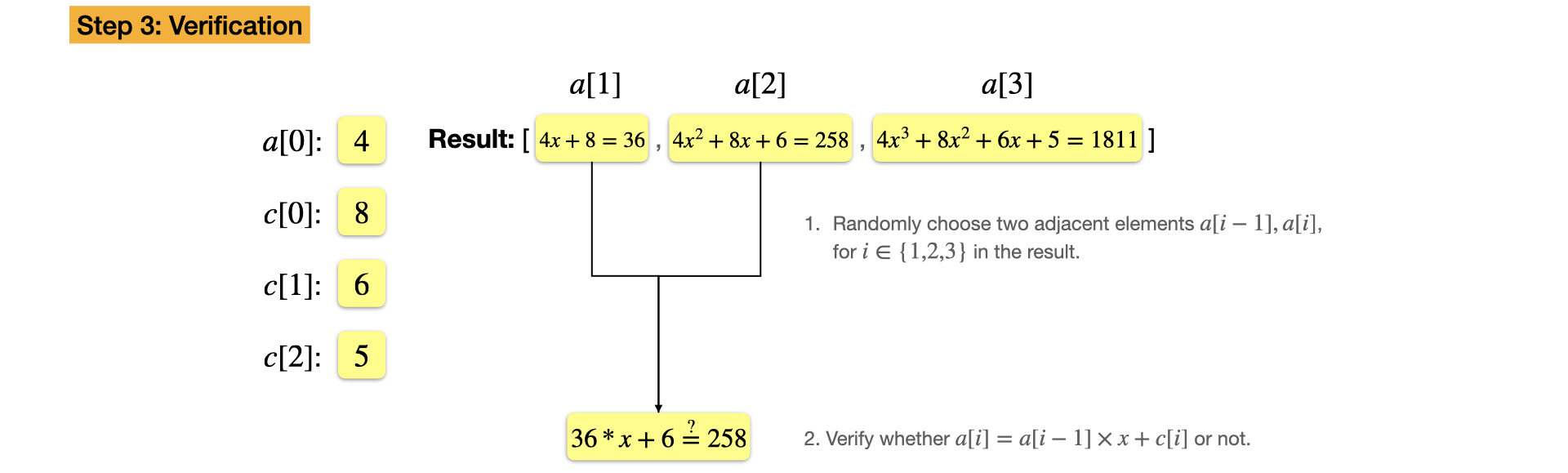
Example: $f(x) = 4 x^3 + 8x^2 + 6x + 5,~x=7$
When $f(x) = \sum_{i = 0}^n a_i x^i$ Is a Sparse Polynomial
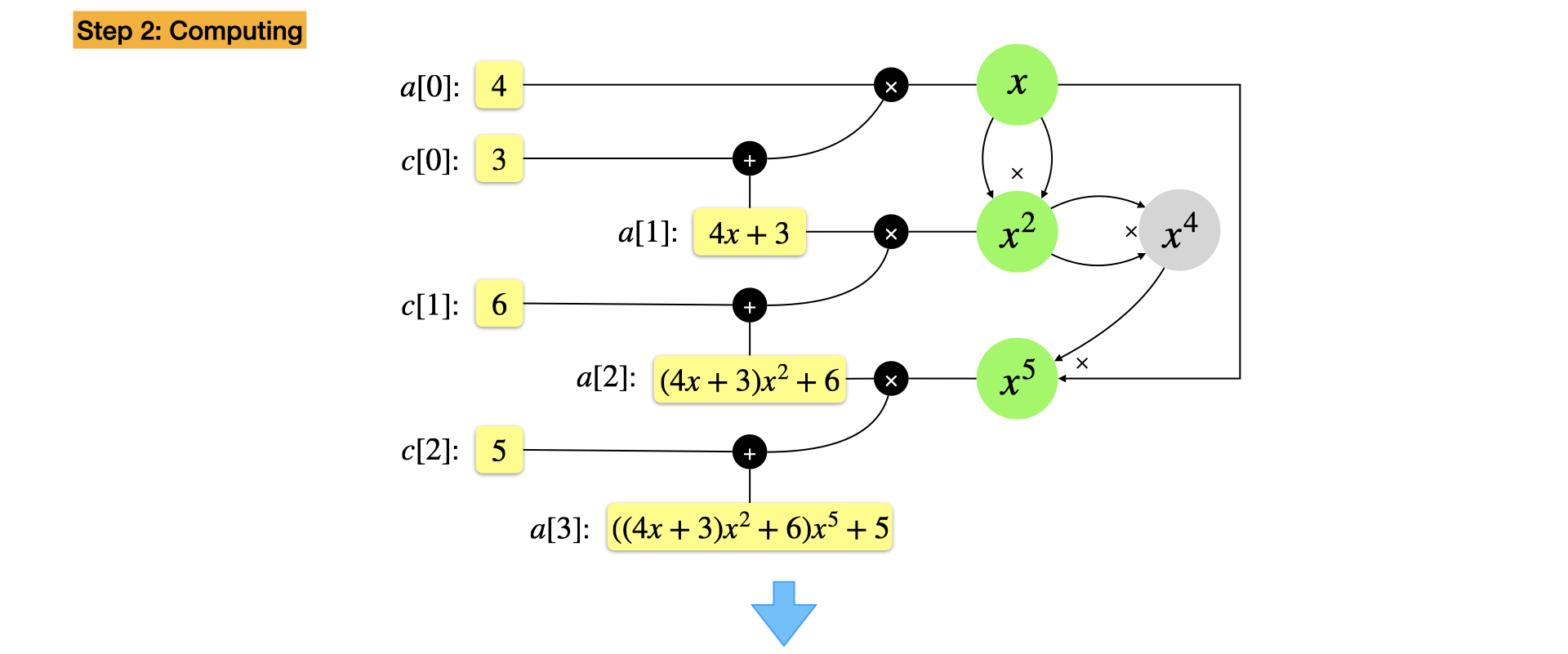
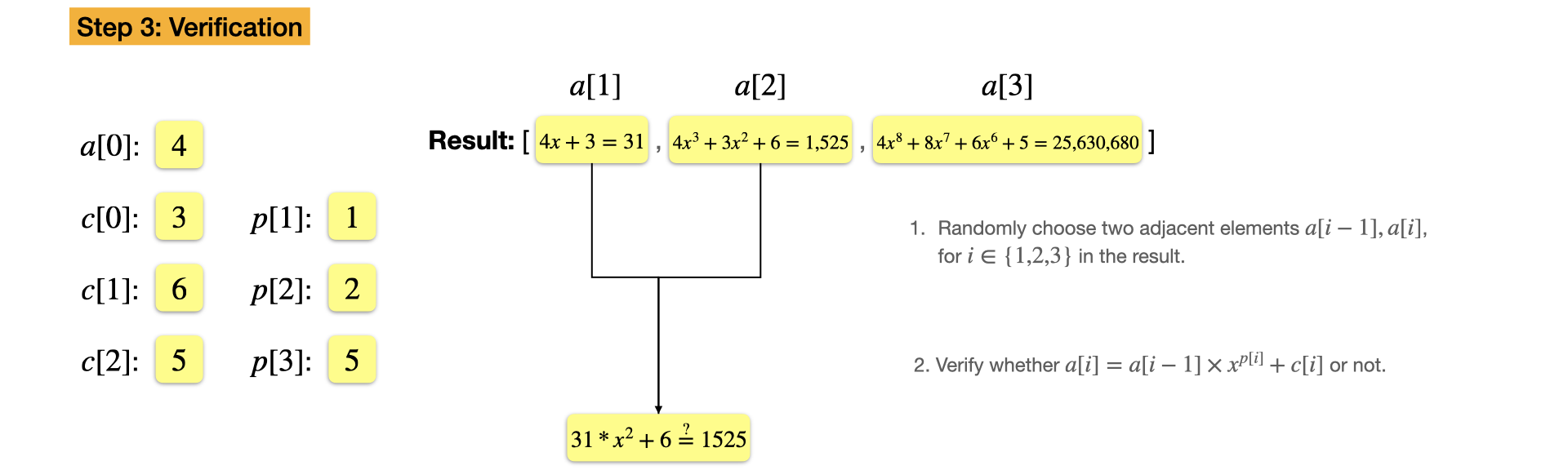
Example: $f(x) = 4 x^8 + 3 x^7 + 6x^5 + 5,~x=7$
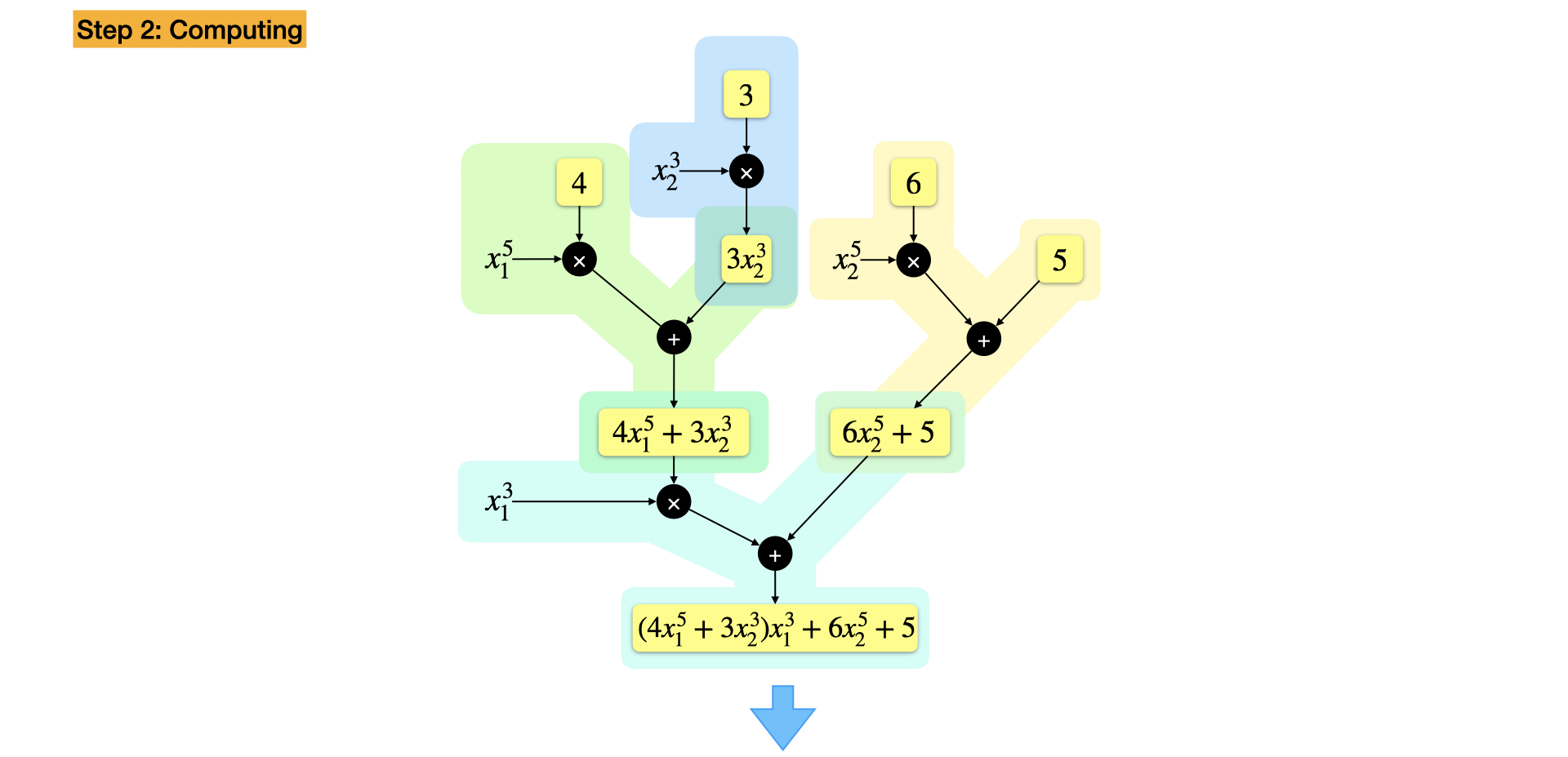
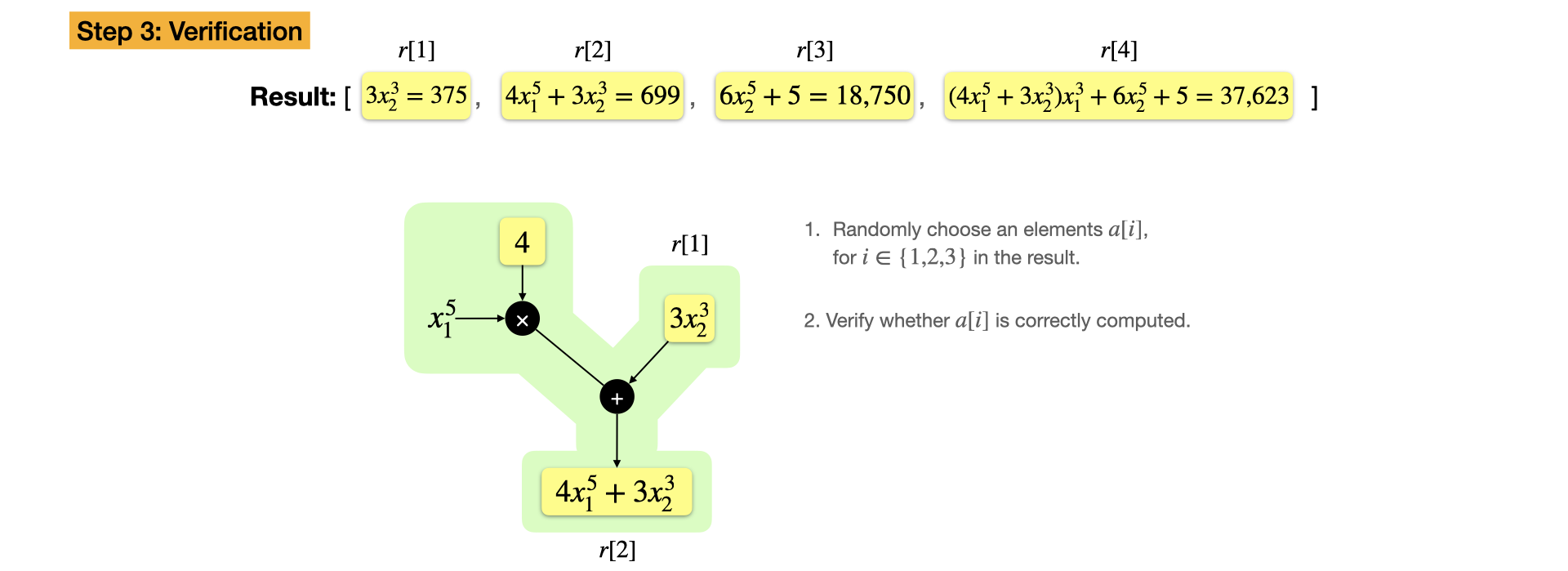
When $f(x) = \sum_{i = 0}^N a_i \prod_{j = 1}^{\tilde{n}} x_{j}^{p_{ij}}$ Is a Multivariate Polynomial
Example: $f(x) = 4 x_1^8 + 3 x_1^3 x_2^3 + 6x_2^5 + 5,~x_1=3,~x_2=5$
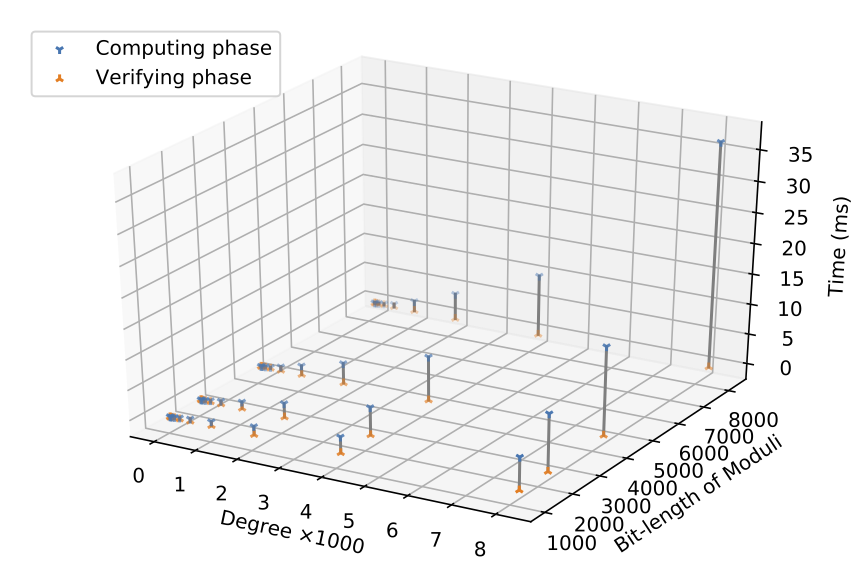
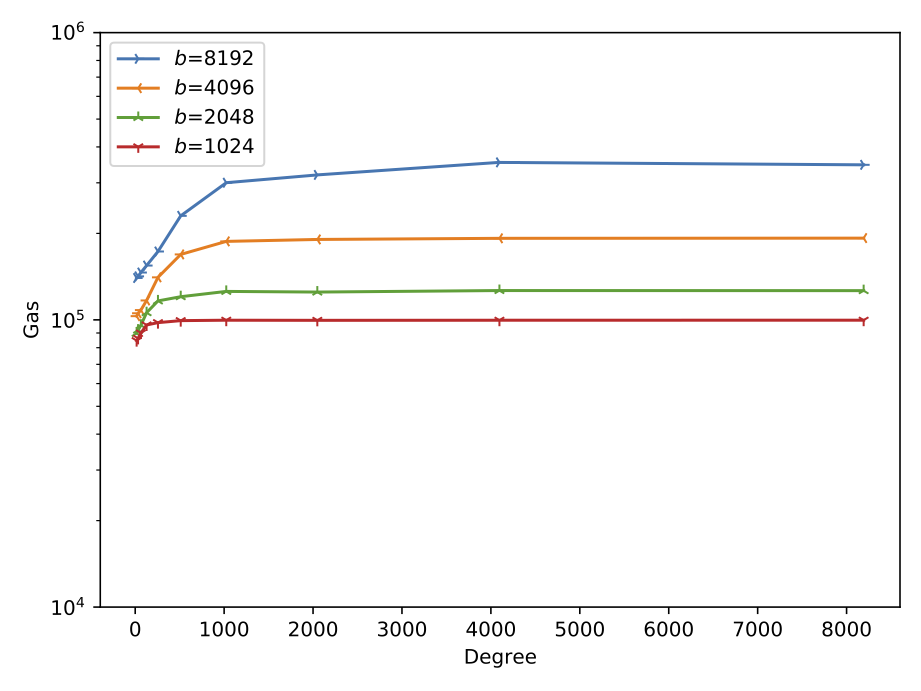
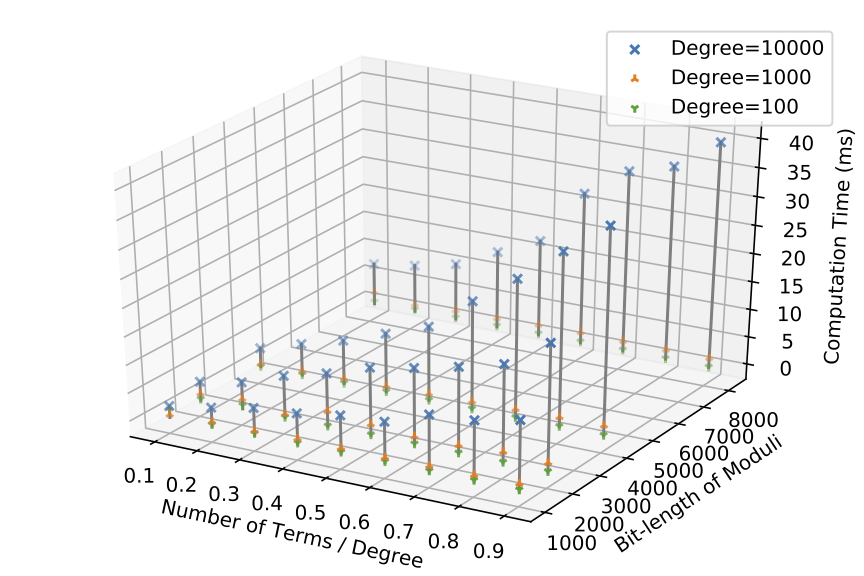
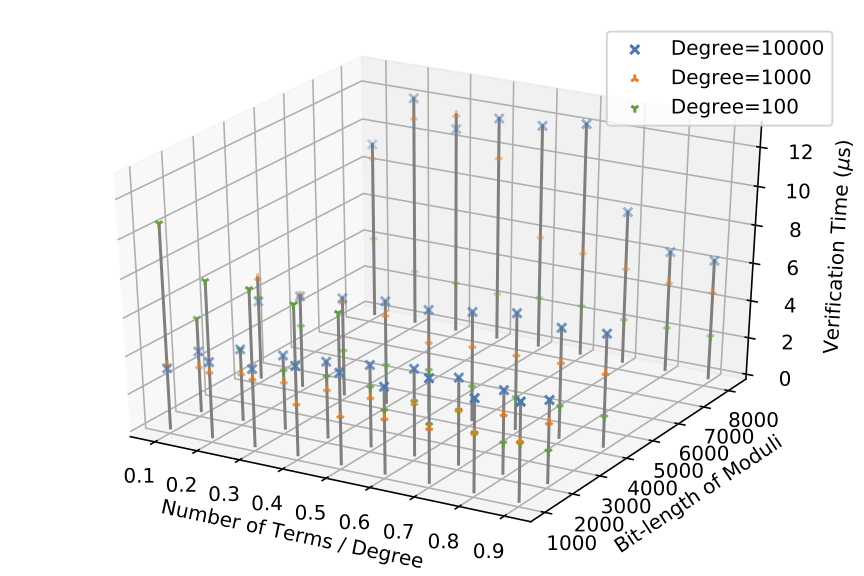
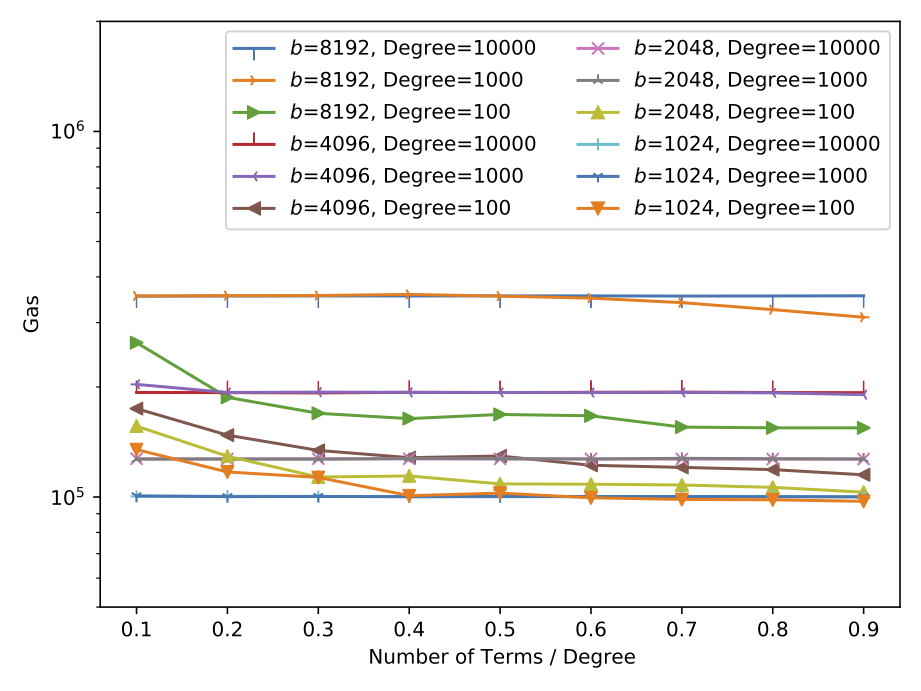
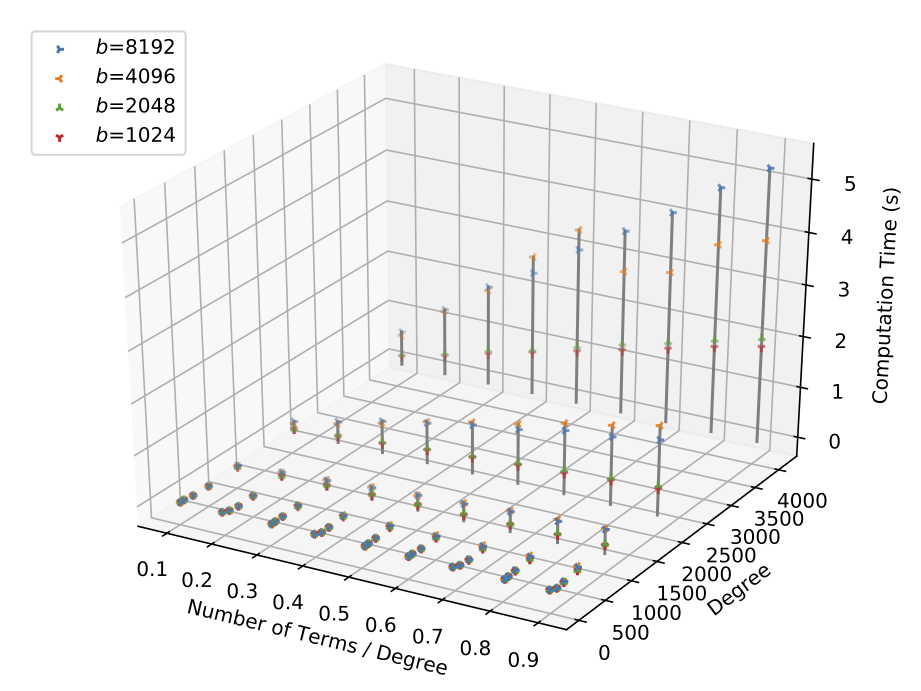
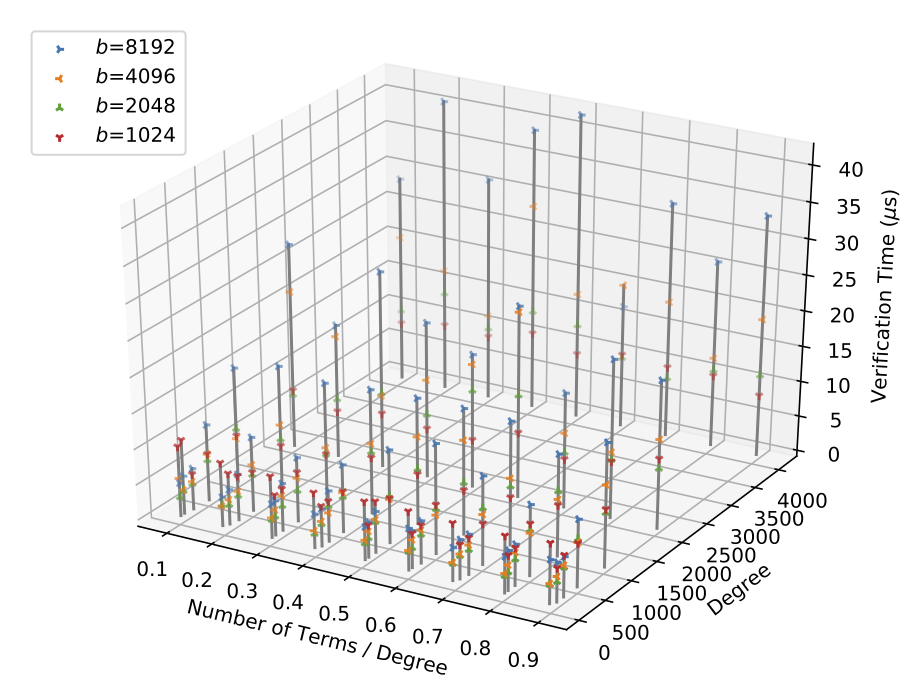
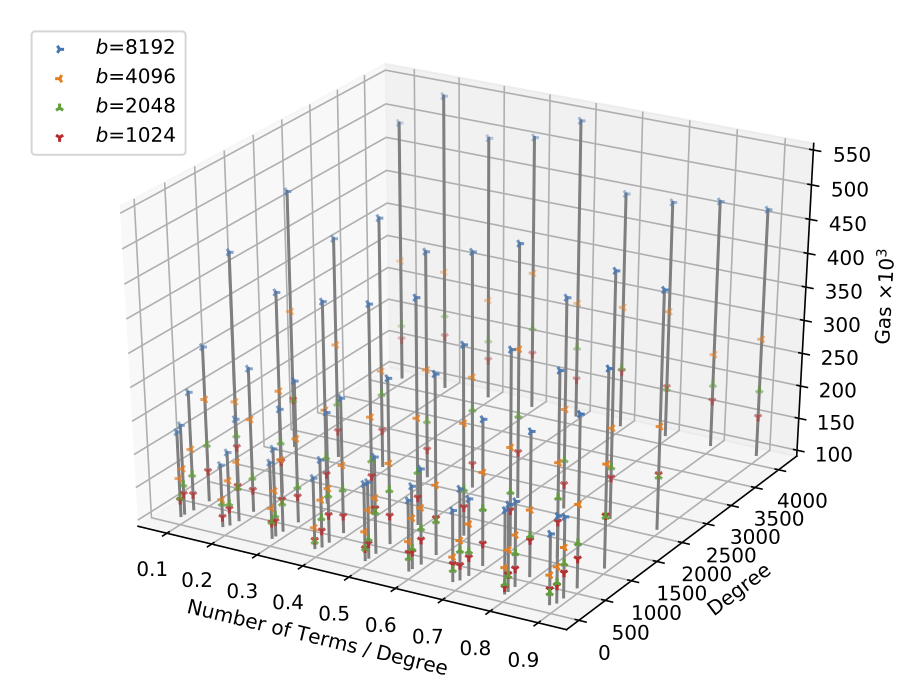
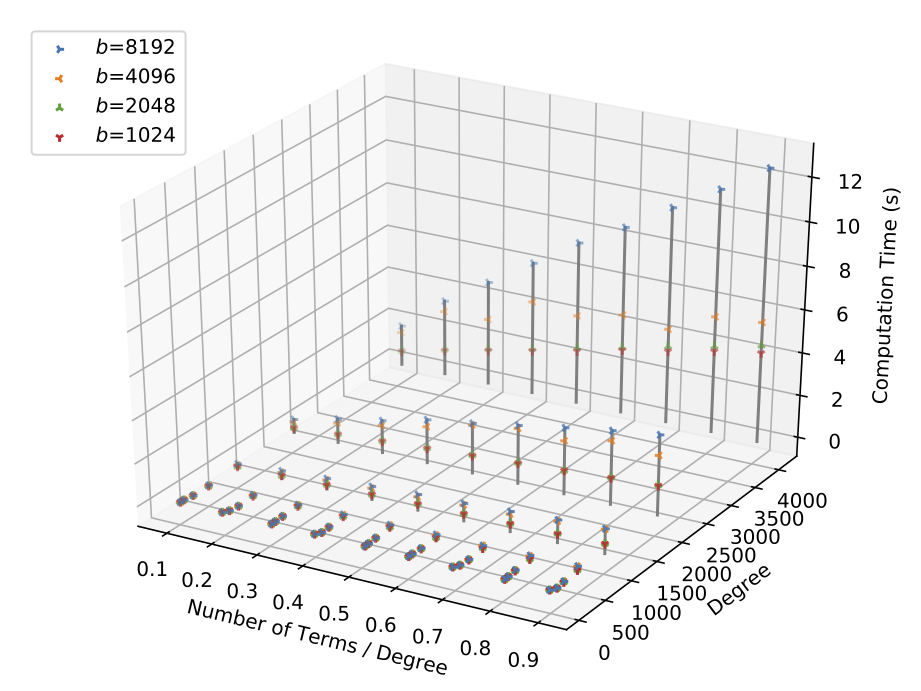
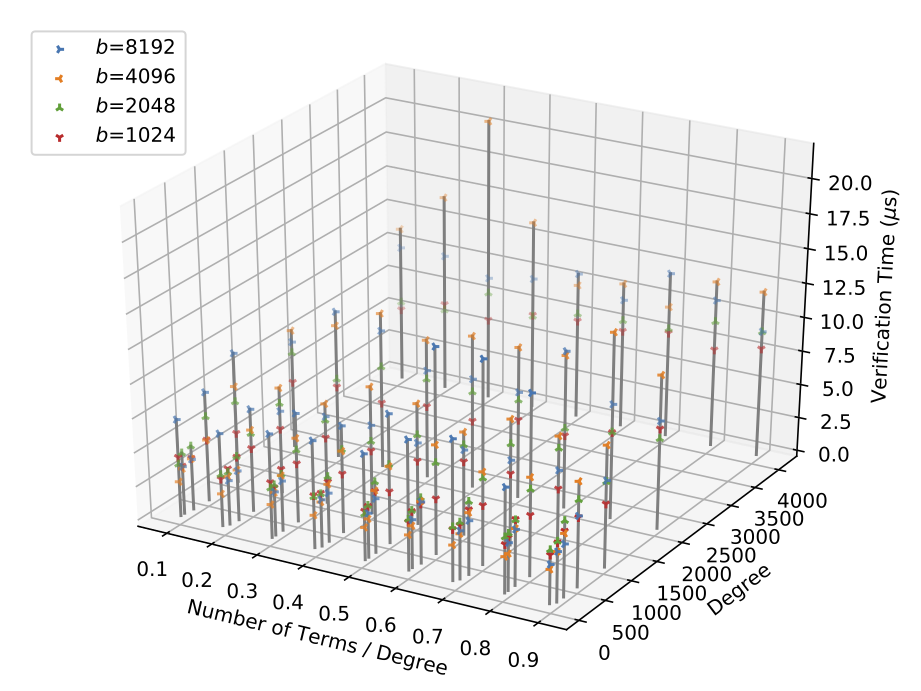
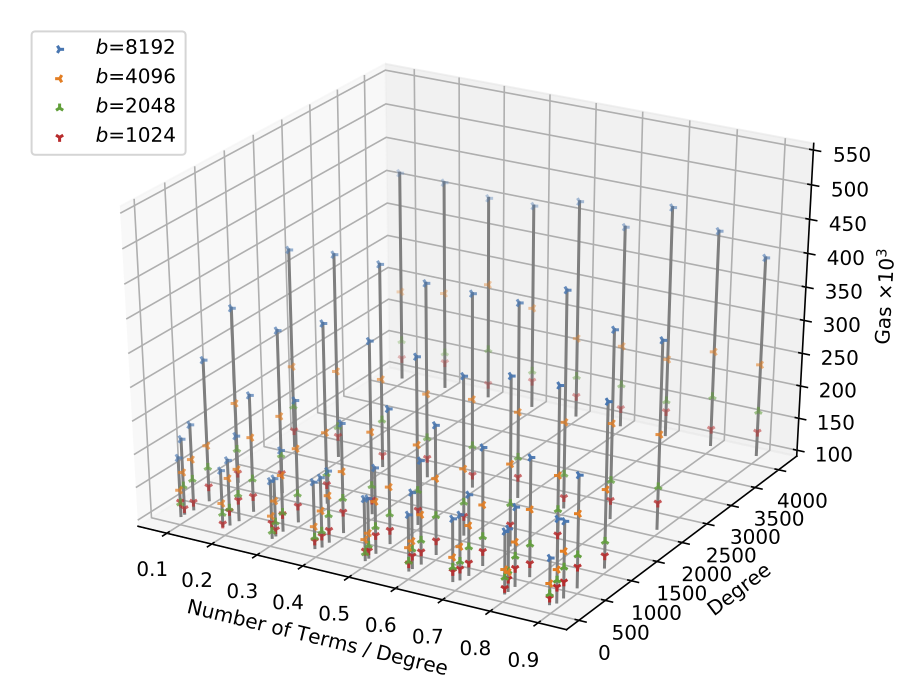
Performance Evaluation
Fig. 1 The computation and verification time for univariate polynomials.
Fig. 2 The gas consumption for univariate polynomials.
Fig. 3 The computation time for sparse univariate polynomials.
Fig. 4 The verification time for sparse univariate polynomials.
Fig. 5 The gas consumption for verifying sparse univariate polynomials.
Fig. 6 The computation time for multivariate polynomials with 2 variables.
Fig. 7 The verification time for multivariate polynomials with 2 variables.
Fig. 8 The gas consumption for verifying multivariate polynomials with 2 variables.
Fig. 9 The computation time for multivariate polynomials with 4 variables.
Fig. 10 The verification time for multivariate polynomials with 4 variables.
Fig. 11 The gas consumption for verifying multivariate polynomials with 4 variables.
Demo download
The sourcecode of this project can be found at guanyg/polyOutsource.